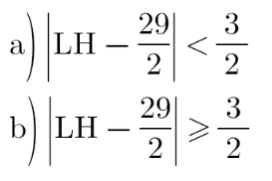Saifulah.id - Assalamualaikum teman-teman, kali ini saya akan membahas penyelesaian soal Matematika, Bab 1 tentang Persamaan dan Pertidaksamaan Nilai Mutlak Linear Satu Variabel, Uji Kompetensi 1 .2, Halaman 37-38, Buku Matematika kelas X (sepuluh) SMA/ MA/ SMK/ MAK.
SOAL
Selesaikanlah soal-soal berikut dengan tepat.
1. Manakah dari pernyataan di bawah yang benar? Berikan alasanmu.
- a) Untuk setiap x bilangan real, berlaku bahwa |x| ≥ 0.
- b) Tidak terdapat bilangan real x, sehingga |x| < –8.
- c) |n| ≥ |m|, untuk setiap n bilangan asli dan m bilangan bulat.
2. Selesaikan pertidaksamaan nilai mutlak berikut.
3. Maria memiliki nilai ujian matematika: 79, 67, 83, dan 90. Jika dia harus ujian sekali lagi dan berharap mempunyai nilai rata-rata 81, berapa nilai yang harus dia raih sehingga nilai rata-rata yang diperoleh paling rendah menyimpang 2 poin?
4. Sketsa grafik y = |3x – 2| – 1, untuk –2 ≤ x ≤ 5, dan x bilangan real.
5. Sketsa grafik y = |x – 2| – |2x – 1|, untuk x bilangan real.
6. Hitung semua nilai x yang memenuhi kondisi berikut ini.
- a) Semua bilangan real yang jaraknya ke nol adalah 10.
- b) Semua bilangan real yang jaraknya dari 4 adalah kurang dari 6.
7. Level hemoglobin normal pada darah laki-laki dewasa adalah antara 13 dan 16 gram per desiliter (g/dL).
- a) Nyatakan dalam suatu pertidaksamaan nilai mutlak yang merepresentasikan level hemoglobin normal untuk laki-laki dewasa.
- b) Tentukan level hemoglobin yang merepresentasikan level hemoglobin tidak normal untuk laki-laki dewasa.
8. Berdasarkan definisi atau sifat, buktikan |a – b| ≤ |a + b|
9. Gambarkan himpunan penyelesaian pertidaksamaan linear berikut ini dengan memanfaatkan garis bilangan.
- a) 4 < |x + 2| + |x – 1| < 5
- b) |x – 2| ≤ |x + 1|
- c) |x| + | x + 1| < 2
10. Diketahui fungsi f(x) = 5 – 2x, 2 ≤ x ≤ 6. Tentukan nilai M sehingga |f(x)| ≤ M. Hitunglah P untuk |f(x)| ≥ P.
KUNCI JAWAB
a. Benar, karena sesuai dengan sifat-sifat nilai mutlak
b. Benar, karena nilai mutlak dari x selalu bilangan postif
c. Tidak benar, karena terdapat (n = 1 ) dan (m = 2) tetapi nilai (n < m)
2.
3. 76 ≤ nilai ≤ 96
4.
5.
6.
a) |x| = 1 0
x = 1 0 atau x = -1 0
b) |x - 4| < 6
-6 < x-4 < 6
-2 < x < 1 0
x = {-1 , 0, 1 , 2, 3, 4, 5, 6, 7, 8, 9}
x = 1 0 atau x = -1 0
b) |x - 4| < 6
-6 < x-4 < 6
-2 < x < 1 0
x = {-1 , 0, 1 , 2, 3, 4, 5, 6, 7, 8, 9}
7.
8. |a - b| ≤ |a + b| apabila a dan b adalah bilang positif
9.
10.
f(2) = 1
f(6) = -7
-7 ≤ f(x) ≤ 1
Sehingga M ≥ 7 dan P ≤ -7
f(6) = -7
-7 ≤ f(x) ≤ 1
Sehingga M ≥ 7 dan P ≤ -7
Selain pembahasan soal Matematika di atas, kalian juga bisa menemukan cara mengerjakan soal MTK lainnya dengan menekan tombol di bawah