Kunci Jawaban Soal MTK Uji Kompetensi 4.5 Halaman 201 -203 Bab 4 Kelas 10 SMA

Saifulah.id - Assalamualaikum siswaku semua, kali ini pak guru akan membahas penyelesaian soal

Matematika, Bab 4 tentang Trigonometri, Uji Kompetensi 4.5, Halaman 201 -203, Buku

Matematika kelas X (sepuluh) SMA/ MA/ SMK/ MAK.

SOAL & KUNCI JAWABAN

1. Jika diketahui segitiga ABC, dengan ukuran panjang sisi dan sudutsudutnya sebagai berikut.

a. b = 20, ∠C = 105°, dan ∠B = 45°. Hitung panjang sisi a dan c.

Jawab:

b. c = 20, ∠A = 35°, dan ∠B = 40°. Hitung panjang sisi a dan b.

Jawab:

c. a = 12,5, b = 10, dan ∠A = 110°. Hitung besar ∠B, ∠C, dan panjang sisi c.

Jawab:

d. a = 4, b = 6, dan ∠C = 120°. Hitung besar ∠A, ∠B, dan panjang sisi c.

Jawab: Kerjakan sendiri

2. Di bawah ini, diketahui panjang sisi-sisi segitiga PQR. Hitung nilai sinus dan tangen untuk setiap sudutnya.
a. p = 10 , q = 14, dan r = 20

Jawab:

b. p = 11 , q = 15, dan r = 21

Jawab:

c. p = 8 , q = 12, dan r = 17

Jawab:

3. Buktikan untuk setiap segitiga ABC sembarang, maka luas segitiga ABC dirumuskan dengan rumus berikut.

a. L = ½ .b.c.sin ∠A

Jawab:

b. L = ½ .a.c.sin ∠B

Jawab:

c. L = ½ .a.b.sin ∠C

Jawab:

4. Dengan rumus luas segitiga pada soal nomor 3, hitunglah luas segitiga untuk setiap ukuran segitiga ABC pada nomor 1.

Jawab:

5. Diketahui segitiga ABC, dengan AB = 20 cm, AC = 30 cm, dan ∠B = 140°. Hitung panjang BC dan ∠A.

Jawab:

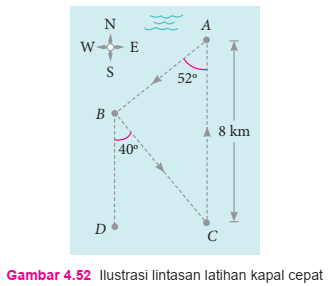
6. Pada latihan mengendarai suatu kapal cepat di perairan, lintasan latihan didesaian seperti yang diberikan pada Gambar 4.52. Pengemudi harus mulai dari titik A, dan bergerak ke arah barat daya dengan membentuk sudut 52° ke titik B, kemudian bergerak ke arah tenggara dengan membentuk sudut 40° ke titik C, dilanjutkan kembali ke titik A. Jarak titik A ke C sejauh 8 km. Hitung panjang lintasan si pengemudi kapal cepat tersebut.

Jawab:

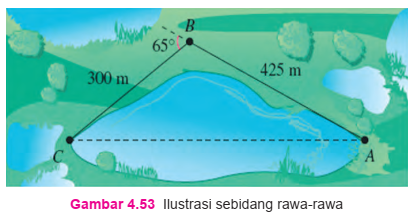
7. Pada saat mensurvei sebidang rawa-rawa, seorang pensurvei berjalan sejauh 425 meter dari titik A ke titik B, kemudian berputar 65° dan berjalan sejauh 300 meter ke titik C (lihat Gambar 4.53). Hitungl panjang AC.

Jawab:

8. Untuk setiap fungsi di bawah ini, manakah yang terdefinisi pada 0o ≤ x ≤ 360°.

a. y = tan x c. y = sec x

Jawab:

b. y = cot x d. y = csc x

Jawab:

c. y = sec x

Jawab:

d. y = csc x

Jawab:

9. Tentukan daerah asal dan daerah hasil untuk setiap fungsi berikut.
a. y = sin x + cos x d. = 1

Jawab:

b. y = sin x – cos x e. = 1

Jawab:

c. y = f. y = sin x + tan x

Jawab: Kerjakan sendiri

Jawab:

Jawab:

f. y = sin x + tan x

Jawab:

10. Gambarkan setiap fungsi f(x) di bawah ini, untuk Df: {0 ≤ x ≤ 2π}.
a. y = 2 sin x d. y = –cos x

Jawab:

y = 2 sin x
⇒ untuk mencari nilai koordinat y nya kita tinggal mengkalikan hasil sin x dengan 2

b. y = sin x + cos x e. y = –tan x

Jawab:

y = sin x + cos x
⇒ sin x dan cos x pada tabel di atas, tinggal kita jumlahkan

c. y = –sin x f. y = 2 + sin x

Jawab:

y = -sin x
⇒ untuk mencari nilai koordinat y nya kita tinggal mengkalikan hasil sin x dengan -1

d. y = –cos x

Jawab:

y = -cos x
⇒ untuk mencari nilai koordinat y nya kita tinggal mengkalikan hasil cos x dengan -1

e. y = –tan x

Jawab:

y = -tan x
⇒ untuk mencari nilai koordinat y nya kita tinggal mengkalikan hasil tan x dengan -1

f. y = 2 + sin x

Jawab:

y = 2 + sin x
⇒ untuk mencari nilai koordinat y nya kita tinggal menjumlahkan hasil sin x dengan 2 atau menggeser grafik sin x ke atas sebanyak 2 satuan.

Selain pembahasan soal Matematika di atas, kalian juga bisa menemukan cara mengerjakan soal MTK lainnya dengan menekan tombol di bawah

Soal Kelas 10 Download Buku