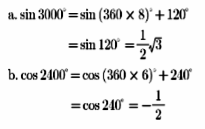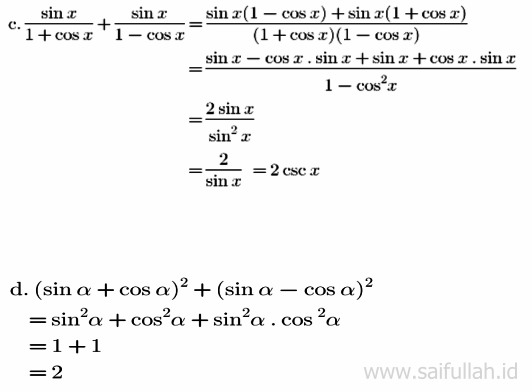SOAL
1. Lengkapi tabel berikut ini.
2. Hitung nilai dari:
a. sin 3.000°
b. cos 2.400°
3. Tentukan 5 nilai perbandingan trigonometri yang lain untuk setiap pernyataan berikut ini.
4. Selidiki kebenaran setiap pernyataan berikut. Berikan alasan untuk setiap jawabanmu.
a. sec x dan sin x selalu mimiliki nilai tanda yang sama di keempat kuadran.
b. Di kuadran I, nilai perbandingan sinus selalu lebih dari nilai perbandingan cosinus.
c. Untuk 30° < x < 90° dan 120° < y < 150° maka nilai 2 sin x < cos² y.
6. Dengan menggunakan identitas trigonometri, sederhanakan setiap bentuk berikut ini.
7. Diketahui α = 45o dan b = 60o. Hitung
a. 2 × sin 45° × cos 60°
b. sin 45° × cos 60° + sin 60o × cos 45°
c. sin 45° × cos 60° – sin 60o × cos 45°
e. sin2 45° + cos² 60° + sin² 60° + cos² 45°
8. Diberikan fungsi f(x) = sin (x + 90°) , untuk setiap 0° ≤ x ≤ 360°. Untuk semua sudut-sudut istimewa, tentukan nilai fungsi.
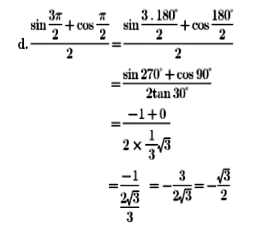
9. Sederhanakan bentuk persamaan berikut ini.
a. cos x . csc x . tan x
b. cos x . cot x + sin x
d. (sin α + cos α)² + (sin α – cos α)²
e. (csc θ – cot θ) × (1 + cos θ)
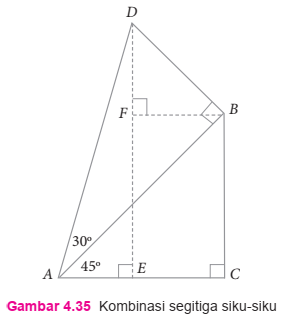
10. Cermati Gambar 4.35. Dengan menemukan hubungan antarsudut-sudut dan panjang sisi-sisi pada segitiga siku-siku yang ada pada gambar, hitung
| a. Panjang AD, EC, BC, BD, AB, FB, AE, dan DE |
c. cos 75°
d. tan 75°
KUNCI JAWABAN
1.
a) sin a > 0 | cos a > 0
sin a bernilai positif jika a berada di kuadran I dan kuadran II
cos a bernilai positif jika a berada di kuadran I dan kuadran IV
karena sin a > 0 dan cos a > 0, maka a berada di kuadran I
b) sin a < 0 | cos a > 0
sin a bernilai negatif jika a berada di kuadran III dan kuadran IV
cos a bernilai positif jika a berada di kuadran I dan kuadran IV
karena sin a < 0 dan cos a > 0, maka a berada di kuadran IV
c) tan a < 0 | sin a > 0
tan a bernilai negatif jika a berada di kuadran II dan kuadran IV
sin a bernilai positif jika a berada di kuadran I dan kuadran II
karena tan a < 0 dan sin a > 0, maka a berada di kuadran II
d) tan a = 0 | sin a > 0
tan a bernilai positif jika a berada di kuadran Idan kuadran III
sin a bernilai positif jika a berada di kuadran I dan kuadran II
karena tan a > 0 dan sin a > 0, maka a berada di kuadran I
e) cosec a < 0 | tan a < 0
cosec a bernilai negatif jika a berada di kuadran III dan kuadran IV
tan a bernilai negatif jika a berada di kuadran II dan kuadran IV
karena cosec a < 0 dan tan a < 0, maka a berada di kuadran IV
2.
3.
4.
a. Tidak
alasan : sec x = 1/ cos x bandingkan dgn sin x
kw I : 1/cos x = +
sin x = +
kw II : 1/cos x = –
sin x = +
(lihat kw II tdk sama tanda, cukup untuk mewakili alasan)
b. Tidak
Alasan : Kw I : sin 30 = 1/2 =0,5
cos 30 = 1/2√3 = 0,86..
Sin 30 < cos 30
(cukup untuk mewakili alasan)
c. Tidak
Alasan :
2 sin x –> misal x = 45
2 sin 45 = 2. 1/2√2 = √2 = 1,414
cos 2y –> misal y = 135
cos 2y = 1- 2 sin²y
= 1 – 2. sin²135
= 1 – 2. sin²45
= 1 – 2. (1/2√2)²
= 1 – 2. 1/4. 2
= 1-1
= 0
sehingga 1,414 < 0 (tidak)
5.
6.
7.
8.
f(x) = sin (x + 90°)
Dengan x adalah sudut istimewa.
Ingat sudut sudut istimewa. Yaitu 0°, 30°, 45°, 60°, dan 90°.
f(0°) = sin (0° + 90°)
f(0°) = sin 90°
f(0°) = 1
f(30°) = sin (30° + 90°)
f(30°) = sin (120°)
f(30°) = ½√3
f(45°) = sin (45° + 90°)
f(45°) = sin 135°
f(45°) = ½√2
f(60°) = sin (60° + 90°)
f(60°) = sin 150°
f(60°) = ½
f(90°) = sin (90° + 90°)
f(90°) = sin 180°
f(90°) = 0
9.
10.
Selain pembahasan soal Matematika di atas, kalian juga bisa menemukan cara mengerjakan soal MTK lainnya dengan menekan tombol di bawah
