Diketahui fungsi 𝑓: 𝑅 → 𝑅 dengan 𝑓 (𝑥) = 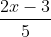 dan fungsi identitas 𝐼: 𝑅 → 𝑅 dengan 𝐼 (𝑥) = 𝑥. Buktikanlah bahwa (𝑓 𝑜 𝐼) = (𝐼 𝑜 𝑓) = 𝑓.
dan fungsi identitas 𝐼: 𝑅 → 𝑅 dengan 𝐼 (𝑥) = 𝑥. Buktikanlah bahwa (𝑓 𝑜 𝐼) = (𝐼 𝑜 𝑓) = 𝑓.
KUNCI JAWABAN
Diketahui f adalah suatu fungsi dan I adalah suatu fungsi identitas.
Jika 𝑅𝐼 ∩ 𝐷𝑓 ≠ 0, maka terdapat suatu fungsi identitas yaitu 𝐼(𝑥) = 𝑥
Sehingga berlaku sifat identitas 𝑓 𝑜 𝐼 = 𝐼 𝑜 𝑓 = 𝑓
Untuk mencari (𝑓 𝑜 𝐼)(𝑥), substitusikan 𝐼(𝑥) = 𝑥 ke 𝑓 (𝑥) maka diperoleh:
𝑓 𝑜 𝐼 (𝑥) = 𝑓 (𝐼(𝑥))
= 𝑓 (𝑥)
= 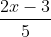
Untuk mencari (𝐼 𝑜 𝑓)(𝑥), substitusikan 𝑓(𝑥) = 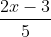 ke 𝐼(𝑥) maka diperoleh:
ke 𝐼(𝑥) maka diperoleh:
(𝑓 𝑜 𝐼)(𝑥) = 𝐼 (𝑓 (𝑥))
= 𝐼 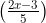
= 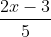
Jadi terbukti bahwa 𝑓 𝑜 𝐼 = 𝐼 𝑜 𝑓 = 𝑓 atau (𝐼 𝑜 𝑓)(𝑥) = 𝑓(𝑥)
Selain pembahasan soal Matematika di atas, kalian juga bisa menemukan cara mengerjakan soal MTK lainnya dengan menekan tombol di bawah

