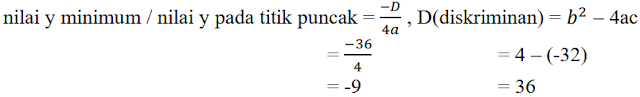Saifulah.id - Assalamualaikum teman-teman, kali ini saya akan membahas penyelesaian soal Matematika, Bab 3 tentang Fungsi, Latihan 3.1 : Memahami Notasi, Domain, Range, dan Grafik Suatu
Contoh
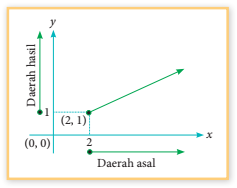
Daerah asal fungsi yang digambarkan pada Gambar 3.2 adalah semua bilangan real x pada interval x ≥ 2, dapat ditulis {x : x ≥ 2} atau x∈(2, ∞). Demikian halnya untuk nilai y, daerah hasilnya adalah semua bilangan real y pada interval y ≥ 1, dapat ditulis {y : y ≥ 1}atau y∈(1, ∞).
Soal
Latihan 3.1
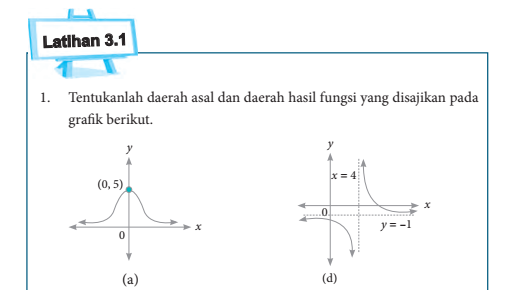
1. Tentukanlah daerah asal dan daerah hasil fungsi yang disajikan pada grafik berikut.
2. Tentukanlah daerah asal dan daerah hasil fungsi berikut.
a. f(x) = 2x + 3
b. f(x) = x2 – 2x – 8
c. f(x) = x2 –1 2 ≤ x ≤ 6
d. f(x) = 2
x(x-5)
x(x-5)
Kunci Jawaban
1. Menentukan daerah asal dan daerah hasil pada kurva
a. Pada gambar, tanda panah yang menuju ke kanan itu artinya x menuju ∞ sedangkan tanda panah yang menuju ke kiri itu artinya x menuju -∞.
Sehingga diperoleh daerah asal : (𝑥 | - ∞ < 𝑥 < ∞) atau (𝑥 |𝑥 ∈ 𝑅)
Untuk mendapatkan daerah hasil perhatikan nilai y. Titik puncak nilai y terdapat pada niai terbesar y karena titik puncak nya berada diatas garis x, yaitu y = 5. Dan untuk nilai terkecil dari y adalah 0.
Sehingga diperoleh daerah hasil : (𝑦 |0 < 𝑦 ≤ 5)
b. Pada gambar, tanda panah yang menuju ke kanan itu artinya x menuju ∞ sedangkan tanda panah yang menuju ke kiri itu artinya x menuju -∞.
Sehingga diperoleh daerah asal : (𝑥 | - ∞ < 𝑥 < ∞) atau (𝑥 |𝑥 ∈ 𝑅)
Untuk mendapatkan daerah hasil perhatikan nilai y. Titik puncak nilai y terdapat pada niai terkecil y karena titik puncak nya berada dibawah garis x, yaitu y = -2. Dan untuk nilai terbesar dari y adalah ∞ karena grafik nya mengarah keatas.
Sehingga diperoleh daerah hasil : (𝑦 |𝑦 ≥ -2)
c. Pada gambar dapat kita peroleh nilai x minimal nya adalah -2 dan x maximal nya adalah 8.
Sehingga dapat kita peroleh daerah asal : (𝑥 | - 2 < 𝑥 ≤ 8)
Lalu dapat kita peroleh nilai y minimal = 1 dan y maximal = 6
Sehingga dapat kita peroleh daerah hasil : (𝑦 |1 < 𝑦 ≤ 6)
d. Untuk daerah asal, terlihat kurva akan menjangkau seluruh sumbu x baik ke kanan maupun ke kiri kecuali pada asimtot tegak nya, yaitu pada sumbu x = 4
Sehingga diperoleh daerah asal : (𝑥 ≠ 4)
Sedangkan untuk daerah hasil, terlihat kurva akan menjangkau seluruh sumbu y baik ke atas maupun ke bawah kecuali pada asimtot datar nya, yaitu pada sumbu y = -1
Sehingga diperoleh daerah hasil : (𝑦 ≠ -1)
e. Pada gambar terlihat bahwa daerah asal kurva tersebut hanya akan menjangkau dari batasan -3 ke kanan (karena kurva mengarah ke kanan)
Sehingga dapat diperoleh daerah asal : (𝑥 ≥ -3)
Sedangkan untuk daerah hasil terlihat bahwa nilai y minimum adalah -5
Sehingga dapat diperoleh daerah hasil : (𝑦 ≥ -5)
f. Untuk daerah asal, terlihat kurva akan menjangkau seluruh sumbu x baik ke kanan maupun ke kiri kecuali pada asimtot tegak nya, yaitu pada sumbu x = -3 dan x = -3
Sehingga dapat diperoleh daerah asal : (𝑥 ≠ -3, 𝑥 ≠ 3)
Sedangkan untuk daerah hasil terlihat bahwa kurva akan menjangkau seluruh sumbu y kecuali pada asimtot datar, yaitu y = 0
Sehingga dapat diperoleh daerah hasil : (𝑦 ≠ 0)
2. Menentukan daerah asal dan daerah hasil pada fungsi
a. f(x) = 2x + 3
fungsi tersebut merupakan fungsi linier yang berbentuk garis lurus, maka fungsi tersebut akan menjangkau seluruh sumbu x.
daerah asal : (𝑥 ∈ 𝑅)
daerah hasil : (𝑦 ∈ 𝑅)
b. f(x) = 𝑥2 - 2𝑥 - 8 → 𝑓(𝑥) = 𝑎2 - 𝑏𝑥 - 𝑐
fungsi tersebut merupakan fungsi kuadrat yang berbentuk parabola. Maka apabila dibuat kurva, akan terlihat bahwa kurva nya terbuka ke atas dan akan menjangkau seluruh sumbu x.
daerah asal : (𝑥 ∈ 𝑅)
daerah hasil : (𝑦 ≥ 9)
c. f(x) = 𝑥2 - 1
daerah asal : (𝑥 ∈ 𝑅)
daerah hasil : (𝑦 ≥ -1)
daerah asal : (𝑥 ∈ 𝑅)
daerah hasil : (𝑦 ≥ -1)
Selain pembahasan soal Matematika di atas, kalian juga bisa menemukan cara mengerjakan soal MTK lainnya dengan menekan tombol di bawah
Mau donasi lewat mana?
BRI - Saifullah (05680-10003-81533)
BCA Blu - Saifullah (007847464643)
Mandiri - Saifullah (1460019181044)
BSI - Saifullah (0721-5491-550)
BCA Blu - Saifullah (007847464643)
Mandiri - Saifullah (1460019181044)
BSI - Saifullah (0721-5491-550)
Merasa terbantu dengan artikel ini? Ayo dukung dengan memberikan DONASI. Tekan tombol merah.
Penulis
PT Saifullah Digital Advantec
Posting Komentar
Popular Emoji: 😊😁😅🤣🤩🥰😘😜😔😪😭😱😇🤲🙏👈👉👆👇👌👍❌✅⭐